启发式算法

启发式算法（heuristic algorithm)是相对于最优化算法提出的。一个问题的最优算法求得该问题每个实例的最优解。启发式算法可以这样定义：一个基于直观或经验构造的算法，在可接受的花费（指计算时间和空间）下给出待解决组合优化问题每一个实例的一个可行解，该可行解与最优解的偏离程度一般不能被预计。现阶段，启发式算法以仿自然体算法为主，主要有蚁群算法、模拟退火法、神经网络等

启发式搜索(Heuristically Search)又称为有信息搜索(Informed Search)，它是利用问题拥有的启发信息来引导搜索，达到减少搜索范围、降低问题复杂度的目的，这种利用启发信息的搜索过程称为启发式搜索。

1)任何有助于找到问题的最优解，但不能保证找到最优解的方法均是启发式方法;
2)有助于加速求解过程和找到较优解的方法是启发式方法。

粒子群优化算法PSO（Particle Swarm Optimization）

算法解释

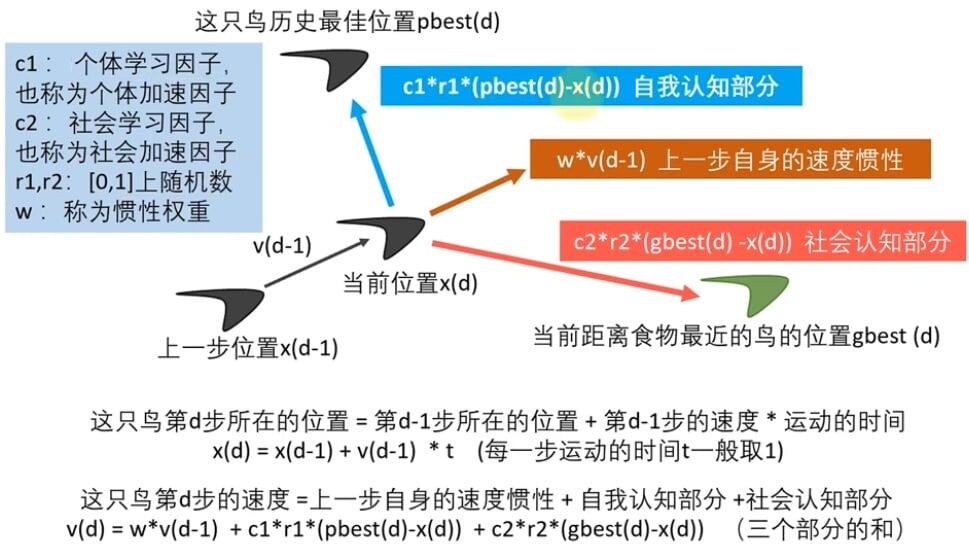
PSO中，每个优化问题的解都是搜索空间中的一只鸟。我们称之为“粒子”。所有的粒子都有一个由被优化的函数决定的适应值(fitnessvalue)，每个粒子还有一个速度决定他们飞翔的方向和距离。然后粒子们就追随当前的最优粒子在解空间中搜索。

粒子群算法图解

核心公式和参数解释

x(d) = x(d-1) + v(d-1)*t（每一步运动的时间 t 一般取1）

v(d)：第d次迭代时，第i个粒子的速度

x(d)：第d次迭代时，第i个粒子所在的位置

v(d) = w*v(d-1) + c1*r1*(pbest(d)-x(d)) + c2*r2*(gbest(d)-x(d))(三个部分的和)

c1：个体学习因子，也称个体加速度因子

c2：社会学习因子，也称社会加速因子

r1,r2：[0,1]上随机数 w：称为惯性权重，一般取0.9就行

pbest：到第d次迭代位置，第i个粒子经过的最好的位置

gbest：到第d次迭代位置，所有粒子经过的最好的位置

粒子：优化问题的候选解位置：候选解所在的位置速度：候选解移动的速度

适应度：评价粒子优劣的值，一般设置为目标函数值f(x)

个体最佳位置：单个粒子迄今为止找到的最佳位置

群体最佳位置：所有粒子迄今为止找到最佳位置

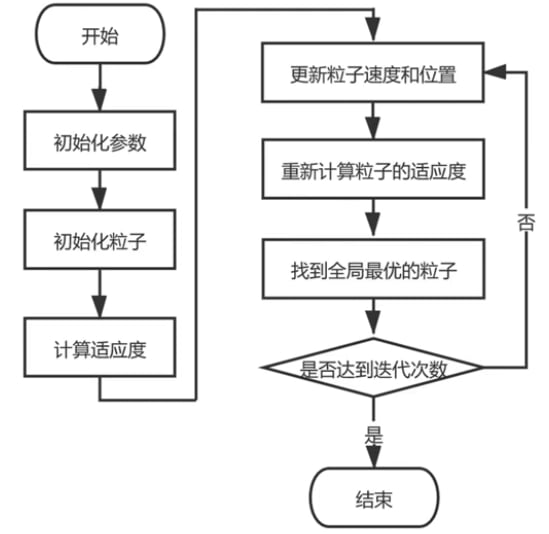
算法流程图

初始化参数：粒子数量，变量个数narvs，c1，c2，w，迭代次数K，最大速度限制vmax(取可行域的10%-20%)，x_lb，x_ub
初始化粒子：每个粒子初始位置d和初始速度v
计算适应度：目标函数f(x)计算fit，pbest，gbest
更新粒子速度和位置：核心公式，v和d是否符合范围
重新计算粒子的适应度：计算第i个粒子的适应度new_fit
找到全局最优的粒子：new_pbest，new_gbest

算法改进1：线性递减递减权重LDIW（Linear Decreasing Inertia Weight）

惯性权重w与迭代次数K有关

较大惯性权重有利于全局搜索
较小惯性权重更利于局部搜索

$w^d = w_{start} - (w_{start} - w_{end}) * \frac{d}{k}$

w~start~ 一般取0.9，w~end~ 一般取0.4

算法改进2：自适应惯性权重

惯性权重w不仅与迭代次数K有关，也与适应度fit有关

1. 最小值问题

适应度越小，说明距离最优解越近，需要局部搜索
适应度越大，说明距离最优解越远，需要全局搜索

$w_i^d = \begin{cases} w_{min} + (w_{max} - w_{min}) * \frac{f(x_i^d) - f_{min}^d}{f_{average}^d - f_{min}^d},&f(x_i^d) \leq f_{average}^d\\ w_{max},&f(x_i^d) > f_{average}^d \end{cases}$

w~max~一般取0.9，w~min~一般取0.4

2. 最大值问题

适应度越大，说明距离最优解越近，需要局部搜索
适应度越小，说明距离最优解越远，需要全局搜索

$w_i^d = \begin{cases} w_{min} + (w_{max} - w_{min}) * \frac{f_{max}^d - f(x_i^d)}{f_{max}^d - f_{average}^d},&f(x_i^d) \geq f_{average}^d\\ w_i^d = w_{max},&f(x_i^d) < f_{average}^d \end{cases}$

算法改进3：随机惯性权重

避免迭代前期局部搜索能力的不足
避免迭代后期全局搜索能力的不足

$w = rand()\\ 或\\ w = μ_{min} + (μ_{max} - μ_{min}) * rand( ) + σ * randn( )$

μ~min~惯性权重最小值0.4，μ~max~为惯性权重最大值0.9，σ(标准差)一般取0.2~05之间

算法改进4：压缩（收缩）因子法

确保PSO算法的收敛性，并可取消对速度的边界限制

$c1 = c2 = 2.05,C = c1 + c2 = 4.1\\ 收缩因子Φ = \frac{2} { |(2-C-\sqrt{C^2-4C})|}$

惯性权重w = 0.9，速度公式更新为：

$v_i^d = Φ*[wv_i^{d-1} + c_1r_1(pbest_i^d - x_i^d) + c_2r_2(gbest^d-x_i^d)]$

算法改进5：非对称学习因子

随着迭代次数增加，使 c1 线性递减，c2 线性递增，从而增强粒子向全局最优点的收敛能力

$c_1^{ini} = 2.5,c_1^{fin} = 0.5,c_2^{ini} = 1,c_2^{fin} = 2.25\\ c_1^d = c_1^{ini} + (c_1^{fin}-c_1^{ini})*\frac{d}{K}; c_2^d = c_2^{ini} + (c_2^{fin}-c_2^{ini})*\frac{d}{K};$

优化问题测试函数

四种常见的测试函数

$函数名&函数表达式&维数&取值范围&理论极值&误差目标\\ Sphere &f(x)=\sum_{i=1}^{n}x_i^2 &30 &[-100,100]^n &0 &10^{-2}\\ Rosenbrock &f(x) = \sum_{i=1}^{n-1}[100(x_{i+1}-x_i^2)^2+(x_i-1)^2] &30 &[-30,30]^n &0 &10^{2}\\ Rastrigin &f(x) = \sum(x_i^2-10cos(2πx_i)=10) &30 &[-5.12,5.12]^n & 0 &10^{2}\\ Griewank &f(x) = \frac{1}{4000}\sum_{i=1}^{n}x_i^2-\prod_{i=1}^{n}cos(\frac{x_i}{\sqrt{i}})+1 &30 &[-600,600]^n &0 &10^{-1}$

算法改进6：自动退出迭代循环

能极大减小迭代的次数，提高运行速度

初始化最大迭代次数、计数器Count以及最大计数值max_Count
定义“函数变化容忍度”tolerance，一般取10^-6
迭代过程中，每次计算出最佳适应度后，计算和上次最佳适应度变化量
判断变化量和“函数变化容忍度”相对大小，如果前者小计数器计1，反之计0
不断重复，有两种可能：
1. 此时没有达到最好迭代次数，计数器值超过了最大计数值，跳出循环，搜索结束
2. 此时已经达到了最大迭代次数，直接跳出循环，搜索结束

Matlab自带的粒子群函数

Matlab中particleswarm函数采用的是自适应的领域模式

默认求最小值

搜索初期使用领域模式lbest
搜索后期是使用全局模式gbest
自适应调整参数
- 适应度开始停滞是，从领域模式转向全局模式
- 适应度开始下降，有回复到领域模式
- 适应度听哈子次数租后大势，惯性系数逐渐变小，利于局部搜索

% particleswarm基础使用1
narvs = 2; % 变量个数
x_lb = [-15 15]; % x的下界（长度等于变量个数，每个变量对于一个下界约束）
x_ub = [15 15]; % x的上界
[x,fval,exitflag,output] = particleswarm(@fun2,narvs,x_lb,x_ub)

% particleswarm基础使用2
narvs = 30;
x_lb = -30*ones(1,30);
x_ub = 30*ones(1,30);
[x,fval,exitflag,output] = particleswarm(@fun3,narvs,x_lb,x_ub)

% 修改函数的参数
%% 绘制最佳函数值岁迭代次数的变化图
options = optimoptions('particleswarm','PlotFcn','pswplotbestf')
[x,fval] = particleswarm(@fun3,narvs,x_lb,x_ub,options)

%% 不考虑计算时间，同时修改三个控制迭代退出的参数
tic
options = optimoptions('particleswarm','FunctionTolerance',1e-12,'MaxStallIterations',100,'MaxIterations',100000);
[x,fval] = particleswarm(@fun3,narvs,x_lb,x_ub,options)
toc

函数中可以调整的参数（可同时修改多个）	option中的设置
绘制最佳的函数值随迭代次数的变化图	‘PlotFcn’,’pswplotbestf’
展示函数的迭代过程	‘Display’,’iter’
修改粒子数量，默认的是：min(100,10*nvars)	‘SwarmSize’,50
在粒子群算法结束后继续调用其他函数进行混合求解	‘HybridFcn’,@fmincon
惯性权重的变化范围，默认的是0.1-1.1	‘InertiaRange’,[0.2 1.2]
个体学习因子，默认的是1.49（压缩因子）	‘SelfAdjustmentWeight’,2
社会学习因子，默认的是1.49（压缩因子）	‘socialAdjustmentWeight’,2
最大的迭代次数，默认的是200*nvar	‘MaxIterations’,10000
领域内粒子的比例 MinNeighborsFraction，默认是0.25	‘MinNeighborsFraction’,0.2
函数容忍度FunctionTolerance, 默认1e-6, 用于控制自动退出迭代的参数	‘FunctionTolerance’,1e-8
最大停滞迭代数MaxStallIterations, 默认20, 用于控制自动退出迭代的参数	‘MaxStallIterations’,50

后续讨论

可以解决非线性问题吗？
- 初始化剔除不满足的粒子
- 在适应度函数上构造惩罚项
可以解决组合优化问题吗？

具有连续型的变量，例如函数最后自的问题，成为连续优化问题

具有离散型变量，例如0-1规划，TPS旅行商问题，成为组合优化问题
- 对原理粒子群算法运动公式和运算符号进行重新定义；
- 利用其他智能算法和粒子群算法结合，进行混合求解；（更好的办法：模拟退火）

粒子群算法进阶应用

求解方程组
多元函数拟合
拟合微分方程